3. Solve side pieces (part 2)
The goal of this section is to complete the solving of the
side pieces
(which was begun in section 1) without mixing up the already ordered
edge pieces.
3.1 Solve side pieces on 2 opposite sides
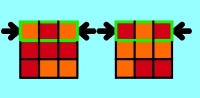
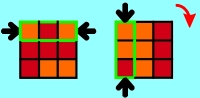
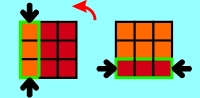
Applet 3a shows the principle way to order the
side pieces:
At first you have to choose 2 opposite sides (for example red and orange) which
should be solved. The side
pieces get solved by exchanging each 3 side
pieces against 3 side
pieces of the opposite side with 180° turns at a
middle layer.
Then a side has to be turned at 90° or 180° that with the next 180° turn at a
middle layer
3 other side pieces
get exchanged.
At the first 180° turn at a middle
layer the edge
pieces which has been solved in section 2 get mixed up again. Therefore you
have to turn away the 4 mixed up edges to the top or to the bottom before you
turn the side which you want to solve. Finally you turn back the edges to its
original positions. Thereby you've reached that at the 180° turns always the
same 4 edges get mixed up. In most cases it is even possible that the edges get
solved with every 2nd 180° turn.
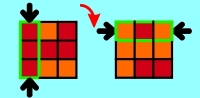
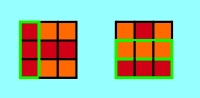
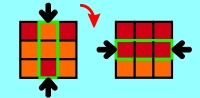
3.1.1 Solve middle 3-piece-combination
Start - exactly like in section 1 - with solving of
the middle 3-piece-combination (consisting of a
center
and 2 edge side pieces).
This should be no problem because there's always only one step necessary (see
applet 3b).
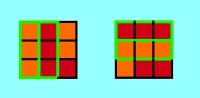
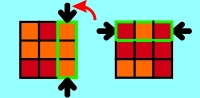
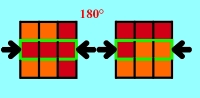
3.1.2 Solve two outer 3-piece-combinations
Now you have to do the most difficult part: In addition to both middle
3-piece-combinations the 2 outer 3-piece-combination (consisting of an
edge side
piece and 2 corner
side pieces) should be also solved. It's difficult in so far as there are
too much possibilities how the Cube looks like at the moment to show a suitable
solution for every conceivable case. Cause in every case 2 steps would be enough
to reach the goal, the chances are pretty well that even those who have
difficulties to get the right solution will reach the goal of this section
after some coincidental chosen exchanges. Therefore I've preliminary limited
the solution to 3 examples (see Applet 3c - 3e). If someone won't reach the goal
after trying for a long time please let me now by sending a mail to
Markus.Pirzer@rubiks.com. If I will
get much mails, I will add a complete overview of all possible cases.
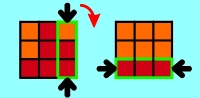
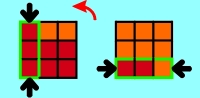
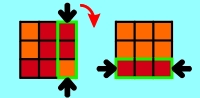
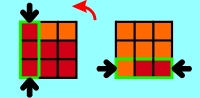
At the following combinations of turns every combination is shown with two
applets: The left applet shows the complete procedure, the right one shows the
same for a better understanding without the necessary inter steps which follow
always the same pattern. You'll find an additional graphical instruction below
both applets: At every step the front and back of the Cube is shown. The
3-piece-combinations which have to be exchanged with the next step are edged
green and marked with black arrows. In addition a red arrow shows - if necessary -
in which direction this side has to be turned by 90° before exchanging. The
instruction "180°" instead of an arrow means that this side has to be turned
at 180°. At each final graphic the ordered 3-piece-combinations are marked with
green margin.
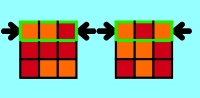
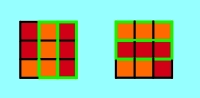
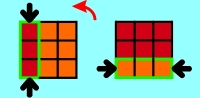
3.1.3 Solve remaining 3-piece-combinations
First get the solved 3-piece-combinations to the same side so that at this
side all 3-piece-combinations are ordered. If both outer 3-piece-combinations
have the same colour (as shown in applet 3h), only the middle 3-piece-combination
needs to be exchanged. Otherwise the Cube looks like in applet 3f or 3g. It is
also possible that the Cube looks like in applet 3f after the first 2 steps. In
this case only the remaining turns of applet 3f need to be done.
3.2 Solve side pieces at the remaining 4 sides
Choose the next 2 opposite sides (in the following called "pair of sides")
which you want to solve, e.g. green and blue. Turn the whole Cube so that the
already solved sides are placed on top and on bottom to avoid that this sides
will get mixed up again. If the edges aren't ordered now, turn it to the
suitable place where they will get ordered with the next turn when you solve the
next pair of sides. There you have to take care that the 4 edges don't change
its relative position to each other. Depending on in which direction you turn
one side (clockwise or counterclockwise) the opposite side has to be turned in
the corresponding direction.
You can leave out the very last turn when you solve the second pair of sides
because this sides will get mixed up when you solve the last pair of sides. Now
solve the last pair of sides also without the last turn. In the ideal case the
last pair of sides need only one turn to be solved and the 4 edges are also
mixed up: In this case one single turn could be enough to complete solving of
the sides. If this case only applies to one pair of sides and the other is
already solved, simply do a 180° turn on a side which should be solved. Thereby
the completely solved pair of sides will reach the desired condition while the
unsolved pair of sides doesn't change its condition because for example 3 white
side pieces
will be exchanged with 3 white side
pieces and 3 yellow side
pieces will be exchanged with 3 other yellow
side pieces. If
all 4 edges are completely solved the same procedure has to be done twice (of
course this time one side of the other pair of sides has to be turned at 180°).
Thereby you reach that the ordered edges will be mixed up while on both pairs of
sides each side piece
will be exchanged with one in the same colours. Now only each 1 side of every
pair of sides has to be turned at 180° (and the necessary inter steps has to be
done as explained under point 3.1) and the sides are perfect. Applet 3i shows
the described worst case: